변분추론
변분추론을 쉽게 설명해봅시다
정확한 사후 분포를 계산하기 어려운 경우, 이를 근사하는 간단한 분포를 찾는 것
변할변變 나눌분分 -> 나누어 변화시키다
뭔가를 조금씩 나누어 변화시키면서 최적의 상태로 추론해나간다
사후 분포: 새로운 정보를 얻은 후에 업데이트된 확률 분포
과자 통에 초콜릿과 바닐라 과자가 있음 <- 사전정보
과자 통에서 과자를 몇 개 꺼내보니 대부분이 초콜릿 <- 새로운 정보
새 정보를 바탕으로 과자 통에 초콜릿 과자가 더 많을 거라고 생각 <- 사후 분포
차이가 클수록 “틀렸다”는 점수 <- 쿨백-라이블러 발산(KL divergence) KL 발산을 줄이는 방향으로 조정
실제 비율: 초콜릿 7,000개 (70%), 바닐라 3,000개 (30%), 총 10,000개
시작:
- 초기 추측: 초콜릿 50%, 바닐라 50%
- 초기 KL 발산: 0.231 (높은 값은 추측이 부정확함을 의미)
1회차 (100개 꺼냄):
- 결과: 초콜릿 73개, 바닐라 27개
- 조정된 추측: 초콜릿 55%, 바닐라 45%
- KL 발산: 0.152
3회차 (총 300개):
- 누적 결과: 초콜릿 212개, 바닐라 88개
- 조정된 추측: 초콜릿 62%, 바닐라 38%
- KL 발산: 0.056
5회차 (총 500개):
- 누적 결과: 초콜릿 354개, 바닐라 146개
- 조정된 추측: 초콜릿 66%, 바닐라 34%
- KL 발산: 0.021
10회차 (총 1,000개):
- 누적 결과: 초콜릿 698개, 바닐라 302개
- 조정된 추측: 초콜릿 69%, 바닐라 31%
- KL 발산: 0.003
15회차 (총 1,500개):
- 누적 결과: 초콜릿 1,052개, 바닐라 448개
- 최종 추측: 초콜릿 70%, 바닐라 30%
- KL 발산: 0.000004 (거의 0에 가까움)
관찰한 데이터를 바탕으로 추측을 계속 개선하면서, 그 차이(KL 발산)를 최소화
1. 변분 추론(Variational Inference)이란?
변분 추론은 복잡한 확률 모델을 간단하게 근사하는 방법입니다. 이는 마치 복잡한 퍼즐을 더 단순한 형태로 바꾸는 것과 비슷합니다.
2. 왜 변분 추론이 필요한가?
- 복잡성 해결: 현실 세계의 많은 문제들은 너무 복잡해서 정확한 계산이 불가능합니다.
- 효율성: 근사적인 방법으로 빠르게 결과를 얻을 수 있습니다.
- 확장성: 대규모 데이터에 적용 가능합니다.
3. 변분 추론의 핵심 아이디어
- 근사: 복잡한 확률 분포를 더 단순한 형태로 근사합니다.
- 최적화: 실제 분포와 근사 분포 사이의 차이를 최소화합니다.
4. 변분 추론의 작동 원리
- 모델 설정: 복잡한 확률 모델을 정의합니다.
- 근사 분포 선택: 단순하지만 유연한 확률 분포를 선택합니다.
- 차이 최소화: 실제 분포와 근사 분포 사이의 차이(KL 발산)를 최소화합니다.
- 반복: 최적의 근사를 찾을 때까지 과정을 반복합니다.
5. 주요 개념
- ELBO (Evidence Lower BOund): 모델의 성능을 측정하는 지표입니다.
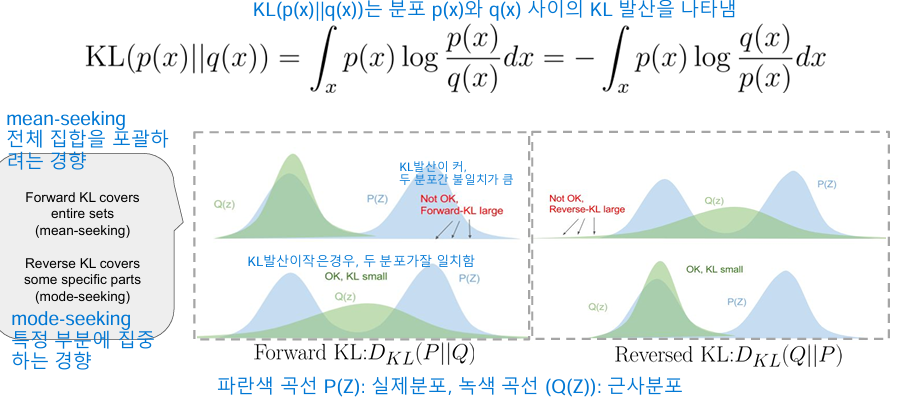
- KL 발산 (Kullback-Leibler Divergence): 두 확률 분포 간의 차이를 측정합니다.
- 평균장 근사 (Mean-Field Approximation): 복잡한 확률 분포를 더 단순한 독립적인 분포들의 곱으로 근사합니다.
6. 변분 추론의 응용
- 토픽 모델링: 대량의 문서에서 주제를 추출합니다.
- 이미지 생성: 새로운 이미지를 생성하는 모델을 학습합니다.
- 추천 시스템: 사용자의 선호도를 예측합니다.
- 자연어 처리: 언어 모델을 개선합니다.
7. 변분 추론의 장단점
장점:
- 복잡한 모델을 다룰 수 있음
- 계산 효율성이 높음
- 대규모 데이터에 적용 가능
단점:
- 정확한 결과가 아닌 근사값을 제공
- 근사의 품질에 따라 결과가 달라질 수 있음
결론
변분 추론은 복잡한 확률 모델을 다루는 강력한 도구입니다. 완벽한 해답을 얻기 어려운 상황에서 실용적이고 효율적인 해결책을 제공합니다. 이는 현대 기계학습과 인공지능의 많은 영역에서 중요한 역할을 하고 있습니다.
L_i: i번째 데이터 포인트에 대한 ELBO
E_q: q 분포에 대한 기대값
p(x_i, z): 실제 결합 확률 분포
q(z): 근사하려는 변분 분포
ELBO는 로그 주변 가능도(log marginal likelihood)의 하한선입니다.
이 값을 최대화함으로써 실제 사후 분포에 가까운 근사를 찾습니다.
계산이 어려운 실제 사후 분포 대신 이 값을 최적화하여 문제를 해결합니다.