변분추론 II
1. MFVI (Mean-Field Variational Inference)
MFVI는 복잡한 확률 분포를 더 단순한 독립적인 분포들의 곱으로 근사하는 방법입니다.
- 비유: 복잡한 퍼즐을 여러 개의 작은 조각으로 나누어 각각 해결하는 것과 비슷합니다.
- 장점: 계산이 간단해지고 빨라집니다.
- 단점: 변수 간의 상호작용을 무시할 수 있어 정확도가 떨어질 수 있습니다.
2. 변분 추론의 응용
2.1 베르누이 혼합 모델 (Mixture of Bernoulli)
- E-step: 각 데이터 포인트가 각 컴포넌트에 속할 확률을 계산합니다 (사후 분포 계산)
- M-step: 이 확률을 바탕으로 모델 파라미터 (ㅠk와 qk)를 업데이트합니다.


- 설명: 여러 개의 동전 던지기 실험이 섞여 있는 상황을 모델링합니다.
- 응용: 이진 데이터(예: 사용자가 아이템을 좋아하는지 여부)를 분석할 때 사용됩니다.
2.2 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)
- 설명: 여러 개의 정규 분포가 섞여 있는 상황을 모델링합니다.
- 응용: 클러스터링, 이미지 분할, 음성 인식 등에 사용됩니다.
2.3 베이지안 가우시안 혼합 모델 (Bayesian Gaussian Mixture Model, BGMM)
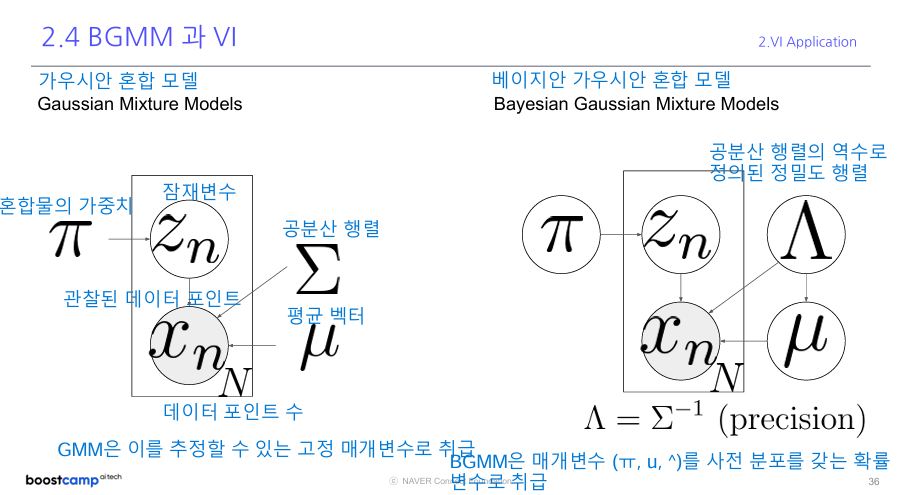
- 설명: GMM에 베이지안 접근법을 적용한 모델입니다.
- 장점
- 초기값에 덜 민감합니다.
- 파라미터의 불확실성을 고려합니다.
- 문제가 될 수 있는 특이점을 피할 수 있습니다.
BGMM에서 정확한 추론이 어려운 이유 BGMM(베이지안 가우시안 혼합 모델)은 데이터를 여러 그룹으로 나누고 각 그룹의 특성을 파악하는 복잡한 통계 모델입니다. 이 모델에서 우리가 알고 싶은 것(예: 각 데이터 포인트가 어느 그룹에 속하는지)을 정확히 계산하려면, 수많은 가능성을 모두 고려해야 합니다. 이는 마치 수백만 개의 퍼즐 조각을 동시에 맞추려는 것과 같아서, 실제로는 불가능합니다.
3. EM 알고리즘과 변분 추론의 비교
- 변분 추론 (A반):
초기 설정: 키와 달리기 속도만을 기준으로 능력을 추정합니다.
1회차:
- 키와 달리기 속도로 빠르게 평가합니다.
- ELBO(추정의 정확도)를 계산하고 기준을 조정합니다.
결과: 6, 4, 8, 6, 3, 7, 5, 5, 9, 2
2회차:
- 조정된 기준으로 다시 평가합니다.
- ELBO를 다시 계산하고 기준을 미세 조정합니다.
결과: 7, 3, 9, 5, 2, 8, 4, 6, 9, 2
VI는 빠르게 대략적인 추정치에 도달합니다.
- EM 알고리즘 (B반):
초기 추측: 모든 학생의 능력을 5로 추측합니다.
1회차:
- E-step: 각 학생을 관찰하고 능력을 추정합니다.
- M-step: 관찰 결과를 바탕으로 추정치를 조정합니다.
결과: 4, 3, 7, 5, 3, 6, 4, 5, 8, 2
2회차:
- E-step: 더 자세히 관찰합니다.
- M-step: 추정치를 다시 조정합니다.
결과: 6, 3, 8, 5, 2, 7, 4, 6, 9, 1
3회차 (최종): 결과: 7, 3, 9, 5, 2, 8, 4, 6, 10, 1
EM은 여러 번의 반복 후에 실제 능력에 매우 가깝게 추정합니다.
주요 차이점:
- 정확도:
- EM(A반)은 최종적으로 거의 정확한 능력치를 얻었습니다.
- VI(B반)는 대체로 비슷하지만 일부 학생(특히 9번, 10번)의 능력을 정확히 파악하지 못했습니다.
- 속도:
- EM은 3번의 상세한 관찰이 필요했습니다.
- VI는 2번의 빠른 평가로 근사한 결과를 얻었습니다.
- 방법:
- EM은 각 학생을 자세히 관찰하여 정확한 사후 분포를 얻으려 했습니다.
- VI는 간단한 기준(키, 달리기 속도)으로 빠르게 근사한 사후 분포를 얻었습니다.
이 예시에서 EM의 “로그 주변 가능도 최대화”는 각 학생의 실제 능력을 정확히 파악하려는 노력을 의미하고, VI의 “ELBO 최대화”는 간단한 기준으로 평가한 결과와 실제 능력의 차이를 최소화하려는 노력을 나타냅니다.
3.1 EM (Expectation-Maximization) 알고리즘
- 목적: 로그 주변 가능도(log marginal likelihood)를 최대화합니다.
- 과정: 기대값 계산(E-step)과 최대화(M-step)를 반복합니다.
3.2 변분 추론 (VI)
- 목적: ELBO(Evidence Lower BOund)를 최대화합니다.
- 특징: 실제 사후 분포를 근사하려고 합니다.
3.3 차이점
- EM은 정확한 사후 분포를 사용하지만, VI는 근사된 사후 분포를 사용합니다.
- VI는 EM보다 더 복잡한 모델에 적용할 수 있습니다.
4. 변분 추론의 최근 응용: 추천 시스템
- 변분 오토인코더(VAE)나 확산 모델(Diffusion Model) 기반의 추천 시스템에서 활용됩니다.
- 사용자의 선호도를 모델링하고 새로운 아이템을 추천하는 데 사용됩니다.
결론
변분 추론 II는 더 복잡한 확률 모델을 다루는 방법을 제공합니다. 이를 통해 현실 세계의 복잡한 데이터를 더 잘 이해하고 분석할 수 있게 됩니다. 특히 추천 시스템과 같은 실제 응용 분야에서 중요한 역할을 하고 있습니다.