몬테카를로 (Monte Carlo) 방법

Exact하게계산이되지않거나,매우오래걸리는연산을randomsampling을통해 근사하는방법론

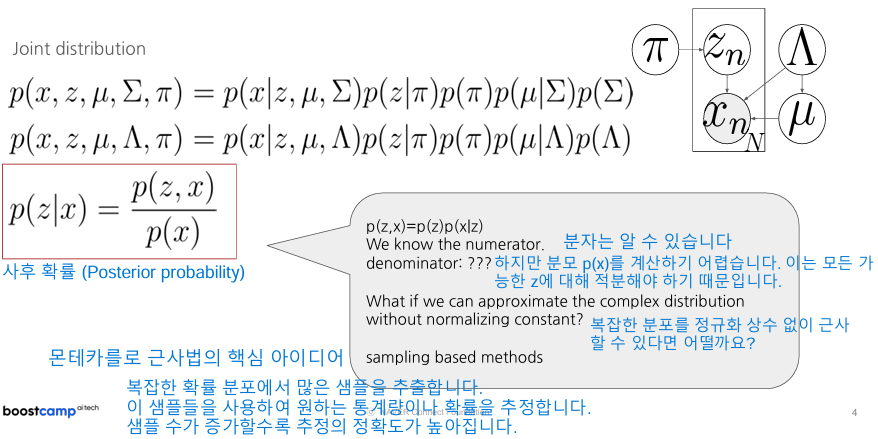
image-20240904182843858

image-20240904182938407

몬테카를로 방법은 복잡한 문제를 무작위 샘플링으로 해결하는 방법입니다. 마치 원 안에 정사각형을 그리고 무작위로 다트를 던져 원의 넓이를 추정하는 것과 비슷합니다.

  • 왜 필요한가?: 수학적으로 정확한 답을 구하기 어렵거나 시간이 너무 오래 걸리는 문제를 빠르게 근사할 수 있습니다.
  • 활용 예: 복잡한 적분 계산, 금융 리스크 분석, 물리 시뮬레이션 등

기각 샘플링 (Rejection Sampling)

원하는 확률 분포에서 직접 샘플을 뽑기 어려울 때 사용하는 방법입니다.

image-20240904183030008

  • 작동 원리:
    1. 간단한 분포에서 샘플을 뽑습니다 (후보 생성)
    2. 일정한 기준으로 샘플을 수용하거나 거부합니다 (심사)
    3. 수용된 샘플만 사용합니다
  • 장점 - 구현이 간단하고 직관적입니다.
  • 단점 - 고차원에서는 효율이 매우 떨어집니다 (대부분의 샘플이 거부됨).

중요도 샘플링 (Importance Sampling)

특정 지역의 평균 만족도를 알고 싶지만, 모든 장소를 다 가볼 수 없을 때 사용하는 전략과 비슷합니다.

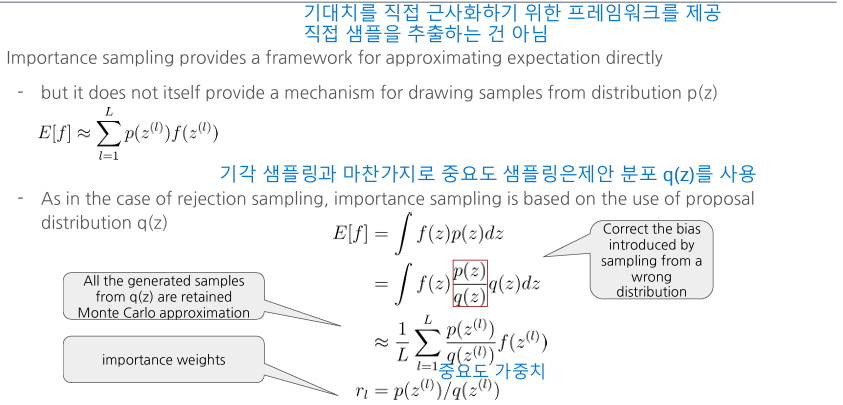
image-20240904183211163

  • 작동 원리:
    1. 쉽게 방문할 수 있는 장소들을 선택합니다 (제안 분포에서 샘플링)
    2. 각 장소의 중요도를 고려해 가중치를 부여합니다
    3. 가중치를 적용해 전체 지역의 만족도를 추정합니다
  • 활용: 희귀 이벤트 시뮬레이션, 컴퓨터 그래픽스의 렌더링 등

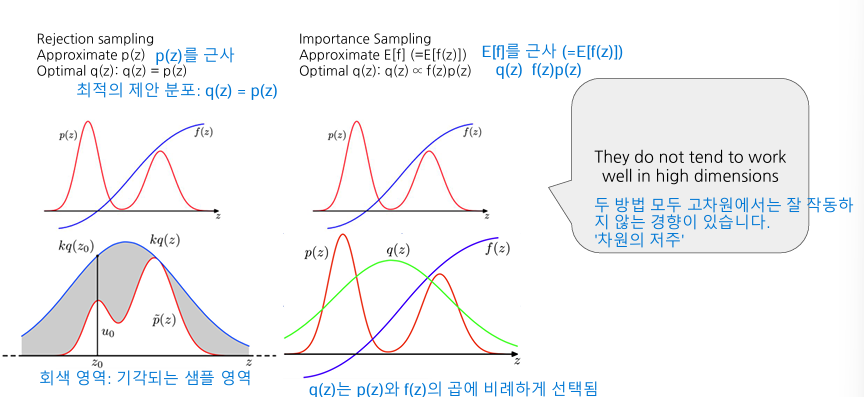
image-20240904183236797

기각 샘플링과 중요도 샘플링는 ‘차원의 저주’로 두 방법 모두 고차원에서는 잘 작동하지 않는 경향이 있음

마르코프 연쇄 몬테카를로 (MCMC)

MCMC는 복잡한 확률 분포에서 효과적으로 샘플을 추출하는 방법입니다. 마치 확률의 풍경을 천천히 산책하며 탐험하는 것과 비슷합니다.

  • 핵심 아이디어:
    1. 현재 상태에서 새로운 상태를 제안합니다.
    2. 제안된 상태를 특정 기준에 따라 수용하거나 거부합니다.
    3. 이 과정을 반복하여 목표 분포에서의 샘플을 얻습니다.
  • 왜 강력한가?:
    • 고차원 공간에서도 효과적으로 작동합니다
    • 복잡한 확률 분포의 특성을 잘 포착할 수 있습니다
    • 수학적으로 정확한 결과를 보장합니다 (특정 조건 하에서)
  • 활용 분야:
    • 베이지안 통계 추론
    • 기계학습 모델의 학습과 추론
    • 복잡한 시스템의 행동 예측

마르코프 연쇄 (Markov Chain)

MCMC의 핵심 개념

마르코프 연쇄는 “현재 상태만 알면 미래를 예측할 수 있다”는 아이디어를 수학적으로 표현한 것입니다.

image-20240904185227081

  • 특징:
    • 다음 상태는 오직 현재 상태에만 의존합니다
    • 과거의 역사는 중요하지 않습니다

  • MCMC와의 관계: MCMC는 특별히 설계된 마르코프 연쇄를 사용해 원하는 확률 분포에서 샘플을 생성합니다.

  • 정상 분포 (Stationary Distribution): 연쇄가 충분히 진행된 후 도달하는 분포입니다.

  • 세부 균형 조건 (Detailed Balance): 정상 분포의 충분 조건으로, MCMC에서 중요한 역할을 합니다.

Metropolis-Hastings 알고리즘

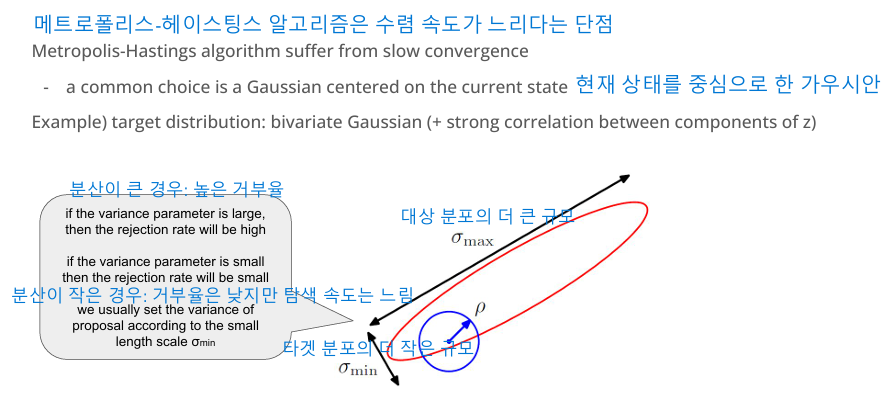
Metropolis-Hastings 알고리즘은 MCMC의 대표적인 방법

알고리즘 단계:

  1. 현재 상태 x에서 제안 분포 q(x’ x)를 사용해 새로운 상태 x’를 제안합니다.

  2. 수용 확률을 계산합니다. \(A(x'|x) = min(1, (π(x') * q(x|x')) / (π(x) * q(x'|x)))\)

  3. 확률 A(x’ x)로 새로운 상태를 수용하고, 그렇지 않으면 현재 상태를 유지합니다.

특징:

  • 제안 분포의 선택이 성능에 큰 영향을 미칩니다.

  • 세부 균형 조건을 만족하여 목표 분포로의 수렴을 보장합니다.

    image-20240904185513661

    image-20240904185418904

Gibbs 샘플링

Gibbs 샘플링은 다변량 분포에서 효과적으로 샘플을 생성하는 MCMC 방법입니다.

작동 원리:

  1. 변수들을 순차적으로 갱신합니다.
  2. 각 변수를 다른 모든 변수가 주어졌을 때의 조건부 분포에서 샘플링합니다.

장점:

  • 조건부 분포가 알려져 있고 쉽게 샘플링할 수 있을 때 매우 효과적입니다.
  • 제안 분포를 설계할 필요가 없습니다.

image-20240904185629307

해밀토니안 몬테카를로 (HMC)

HMC는 MCMC의 발전된 형태로, 물리학의 해밀토니안 역학을 활용합니다.

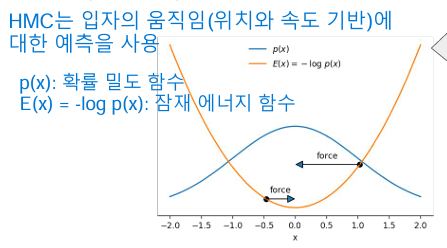
image-20240904185742673

주요 특징:

  • 위치(q)와 운동량(p) 두 가지 변수를 사용합니다.
  • 그래디언트 정보를 활용하여 더 효율적으로 샘플을 생성합니다.

HMC의 기본 단계:

  1. 운동량을 무작위로 생성합니다.
  2. 해밀토니안 역학을 통해 시스템을 진화시킵니다.
  3. Metropolis 수용 단계를 적용합니다.

해밀토니안 동역학 (Hamiltonian Dynamics)

해밀토니안 동역학은 HMC의 핵심 요소입니다.

  • 해밀토니안: H(q, p) = U(q) + K(p)
  • U(q): 퍼텐셜 에너지, K(p): 운동 에너지

해밀토니안 방정식: \(dq/dt = ∂H/∂p dp/dt = -∂H/∂q\) 이 방정식들은 시스템의 시간에 따른 진화를 기술합니다.

HMC 수렴

HMC가 목표 분포로 수렴함을 보이기 위해 다음을 증명합니다:

  1. HMC로 생성된 샘플들이 마르코프 연쇄를 형성합니다.
  2. 이 마르코프 연쇄가 세부 균형 조건을 만족합니다.

세부 균형 증명의 핵심:

  • 해밀토니안 동역학의 가역성을 이용합니다.
  • 에너지 보존 법칙을 활용합니다.

HMC는 MCMC의 강력한 확장으로, 물리학의 개념을 활용하여 효율적인 샘플링을 가능하게 합니다. 기본적인 MCMC 방법들의 한계를 극복하고, 특히 고차원 문제에서 뛰어난 성능을 보입니다.