Neural Network
오늘의 느낀 점
진짜 왤케 졸리냐. 이론이라 그런가.
선요약
| 활성화 함수 | 수식 | 출력 범위 | 장점 | 단점 |
|---|---|---|---|---|
| Sigmoid | σ(x) = 1 / (1 + e^(-x)) | [0, 1] | - 출력이 확률로 해석 가능 - 부드러운 그래디언트 |
- Vanishing gradient 문제 - 출력이 zero-centered 아님 - exp() 연산 비용 높음 |
| Tanh | tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x)) | [-1, 1] | - Zero-centered 출력 - Sigmoid보다 더 가파른 미분 |
- Vanishing gradient 문제 여전히 존재 |
| ReLU | f(x) = max(0, x) | [0, ∞) | - 계산 효율적 - 빠른 수렴 - Sparse activation |
- Dead ReLU 문제 - 출력이 zero-centered 아님 |
| Leaky ReLU | f(x) = max(αx, x), α ≈ 0.01 | (-∞, ∞) | - ReLU의 장점 대부분 유지 - Dead ReLU 문제 해결 |
- 추가 하이퍼파라미터 α |
| ELU | f(x) = x if x ≥ 0 else α(e^x - 1) | (-α, ∞) | - ReLU의 장점 유지 - 음수 입력에 대해 부드러운 saturated 값 |
- exp() 연산 비용 |
선형 모델 (Linear Model)
1.1 선형 모델의 기본 구조
\[f(x,W) = Wx + b\]x는 입력 이미지, W는 가중치(weight), b는 편향(bias)
Softmax 함수를 통해 출력값을 확률로 변환 파라미터들은 (Stochastic) Gradient Descent를 통해 최적화
1.2 선형 분류기 (Linear Classifier)의 한계
- 각 클래스당 하나의 템플릿만 학습 가능
- 직선 형태의 결정 경계(decision boundary)만 그릴 수 있어 복잡한 관계를 완벽히 분리하기 어려움
1.3 특징 (Features)
입력을 직접 출력에 매핑하는 대신 특징을 추출하여 표현 특징 공간 (feature space) 에서 선형 분류가 가능하다면 선형 분류기가 잘 작동
1.4 이미지 특징 (Image Features)
- 색상 히스토그램 (Color histogram)
- 방향 그래디언트 히스토그램(HoG)
- Bag of Words(BoW) 등의 방법으로 이미지 특징을 추출 가능
신경망 (Neural Networks)
퍼셉트론 (Perceptron)
생물학적 뉴런에서 영감을 받은 인공 뉴런 모델 입력값에 가중치를 곱하고 활성화 함수를 통과시켜 출력을 생성
다층 퍼셉트론 (Multilayer Perceptron, MLP)
입력층, 은닉층, 출력층으로 구성된 더 복잡한 신경망 구조
활성화 함수 (Activation Functions)
Sigmoid, tanh, ReLU 등 다양한 활성화 함수
비선형성을 추가하여 신경망의 표현력을 높이는 역할
Forwad pass
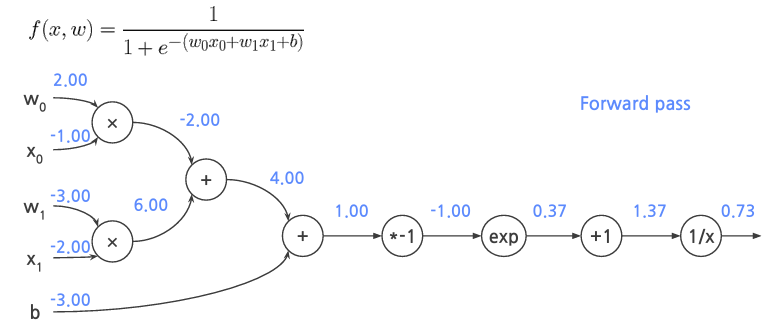
위에있는걸 기호를 미분해서 Backpropagation
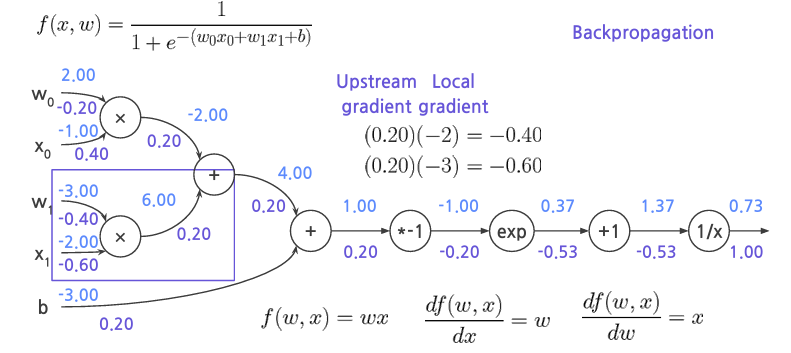
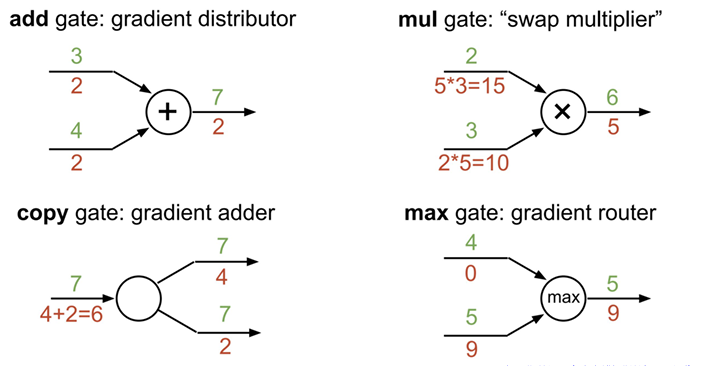
활성화 함수
활성화 함수는 신경망에 비선형성을 부여하는 요소
Sigmoid 함수
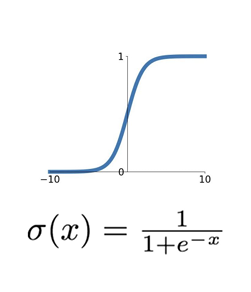
특징:
출력 범위: [0, 1] 과거에 가장 많이 사용되었던 함수
단점:
Vanishing Gradient: 입력이 매우 크거나 작을 때 기울기가 0에 가까워짐 출력값이 zero-centered되지 않음 exp() 연산이 비교적 복잡
Tanh 함수
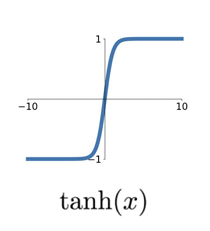
특징:
출력 범위: [-1, 1] Zero-centered 출력
단점:
Vanishing Gradient 문제가 여전히 발생합니다.
ReLU (Rectified Linear Unit)
특징:
양수 영역에서 saturate되지 않습니다. 연산이 매우 효율적입니다. Sigmoid나 Tanh보다 빠르게 수렴합니다.
단점:
출력값이 zero-centered되지 않습니다. Dead ReLU problem: 음수 입력에 대해 항상 0을 출력합니다.
Leaky ReLU
특징:
ReLU의 장점을 대부분 가집니다. Dead ReLU 문제를 해결합니다.
단점:
추가적인 하이퍼파라미터 (alpha)가 필요합니다.
ELU (Exponential Linear Unit)
특징:
ReLU의 모든 장점을 가집니다. 음수 영역에서 부드러운 saturated 값을 가집니다.
단점:
exp() 연산이 필요합니다.
실제로는 ReLU를 주로 사용하며, 학습률에 주의를 기울이는 것이 좋습니다. Sigmoid나 Tanh는 주로 마지막 층에서만 사용됩니다.
가중치 초기화 (Weight Initialization)
작은 가우시안 랜덤 (Small Gaussian Random)
얕은 신경망에서는 잘 작동하지만, 깊은 신경망에서는 문제가 발생합니다. 활성화 값이 0에 가까워져 그래디언트가 사라질 수 있습니다.
큰 가우시안 랜덤 (Large Gaussian Random)
활성화 값이 극단적으로 커지거나 작아질 수 있습니다. 그래디언트가 사라지는 문제가 여전히 발생할 수 있습니다.
Xavier 초기화
모든 층에서 적절한 크기의 활성화 값을 유지할 수 있습니다. 합성곱 층에서는 d_in = F^2 * C (F: 필터 크기, C: 채널 수)로 계산합니다. 현재 가장 널리 사용됨
학습률 조정 (Learning Rate Scheduling)
학습률은 옵티마이저가 파라미터를 얼마나 크게 업데이트할지 결정
적절한 학습률 선택과 조정은 학습 성능에 큰 영향을 미침
학습률 선택 방법
너무 높은 학습률: loss가 급증할 수 있습니다. 너무 낮은 학습률: loss가 천천히 감소합니다. 일반적으로 큰 초기 학습률에서 시작해 점차 감소시킵니다.
학습률 감소 방법
Step Decay
특정 학습 포인트에서 학습률을 감소시킵니다. 예: 50%와 75% 지점에서 학습률을 0.1배로 줄입니다.
Initial Warmup
처음에는 매우 작은 학습률로 시작해 선형적으로 증가시킵니다. 전체 학습의 약 10%에서 warmup이 발생합니다.
기타 감소 방법
Cosine Decay Linear Decay Inverse Square Root Decay
데이터 전처리 (Data Preprocessing)와 데이터 증강 (Data Augmentation)
데이터 전처리 (Data Preprocessing)
X -= np.mean(X, axis=0) # Zero-centering
X /= np.std(X, axis=0) # Normalization
모든 특성의 평균을 0으로 만들어 데이터를 중앙에 위치시킵니다.
각 특성의 스케일을 동일하게 만들어 학습을 안정화합니다.
PCA (주성분 분석): 데이터의 주요 축을 찾아 차원을 줄이거나 특성을 변환합니다.
Whitening: 모든 특성의 분산을 1로 만들어 동등한 중요도를 갖게 합니다.
데이터 증강 (Data Augmentation)
수평 뒤집기 (Horizontal Flips)
이미지를 좌우로 뒤집어 새로운 훈련 데이터를 생성합니다. 단, 의미가 변하지 않는 경우에만 사용해야 합니다.
랜덤 크롭 (Random Crops)
이미지의 일부분을 무작위로 잘라내어 사용합니다. 이는 모델이 객체의 부분적인 특징을 학습하는 데 도움을 줍니다.
스케일링 (Scaling)
이미지의 크기를 변경하여 다양한 스케일에서의 특징을 학습하게 합니다.
색상 변조 (Color Jitter)
이미지의 색상, 채도, 명도를 무작위로 변경합니다. 이는 모델이 다양한 조명 조건에서도 robust하게 만듭니다.