Linear Regression, ML algorithm
선요약
1. 머신러닝
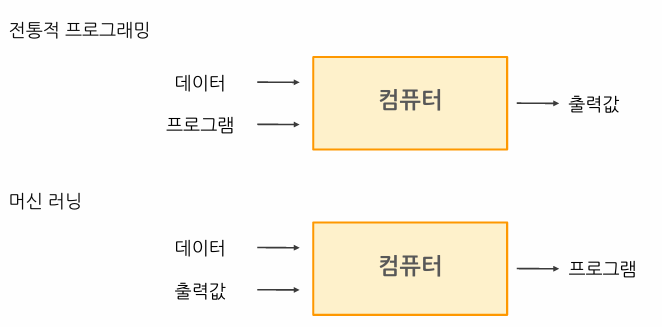
머신러닝은 인공지능의 한 분야로, 데이터로부터 학습하여 성능을 향상시키는 알고리즘을 연구하는 학문
Experience, Tasks, Performance
이미지 분류 작업으로 예를 들면
작업(T): 이미지가 고양이인지 개인지 분류
경험(E): 라벨이 있는 고양이와 개 이미지 데이터셋
성능(P): 분류 정확도
머신러닝의 종류
지도 학습 (Supervised Learning)
입력 데이터와 그에 대응하는 레이블(출력)이 주어짐
목표: 입력을 출력에 매핑하는 함수를 학습
예시: 회귀(Regression): 연속적인 출력값 예측 (예: 주택 가격)
분류(Classification): 이산적인 클래스 예측 (예: 스팸 vs 정상 이메일)
비지도 학습 (Unsupervised Learning)
레이블이 없는 데이터만 주어짐
목표: 데이터의 숨겨진 구조나 패턴을 발견
예시: 고객 세그먼테이션, 이상 탐지
강화 학습 (Reinforcement Learning)
에이전트가 환경과 상호작용하며 행동을 학습
목표: 보상을 최대화하는 정책(policy)을 학습
예시: 게임 플레이 (AlphaGo), 로봇 제어, 자율 주행
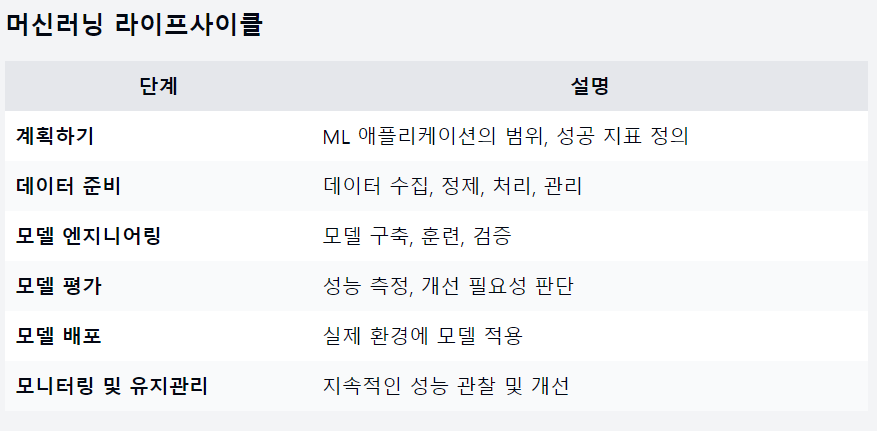
머신러닝 라이프사이클
모델을 개발, 배포, 유지보수하는 전체과정을 포함
- 계획하기 (Planning)
- 데이터 준비 (Data Preparation)
- 모델 엔지니어링 (Model Engineering)
- 모델 평가 (Model Evaluation)
- 모델 배포 (Model Deployment)
- 모니터링 및 유지관리 (Monitoring and Maintenance)
2. Linear Regression (선형 회귀)
회귀 분석: 독립 변수와 종속 변수사이의 관계를 모델링하는 통계적 방법
기본 형태의 방정식
\(y = mx + b\)
y: 종속 변수 (예측하려는 값), x: 독립 변수, m: 기울기 (회귀 계수), b: y 절편 (상수항)
다중 선형 회귀인 경우 \(y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε\)
β₀, β₁, …, βₙ은 회귀 계수이고, ε은 오차항
Linear Regression의 가정
Linear Regression 모델은 다음과 같은 주요 가정을 기반
a) 선형성: 독립 변수와 종속 변수 사이에 선형 관계가 있어야 함
b) 독립성: 관측값들은 서로 독립적이어야 함
c) 등분산성: 모든 독립 변수 값에 대해 오차의 분산이 일정해야 함
d) 정규성: 오차가 정규 분포를 따라야 함
최소 제곱법
Linear Regression에서 가장 일반적으로 사용되는 파라미터 추정 방법
실제 관측값과 모델의 예측값 사이의 차이(잔차)의 제곱합을 최소화하는 방식
\[Σ(y_i - ŷ_i)²\]y_i는 실제 관측값이고, ŷ_i는 모델의 예측값
모델 평가 지표
- 평균 절대 오차 (MAE: Mean Absolute Error)
장점: 해석이 쉽고, 이상치에 덜 민감함
단점: 오차의 방향을 고려하지 않음
- 평균 제곱 오차 (MSE: Mean Squared Error)
장점: 큰 오차에 더 큰 패널티를 부여
단점: 원래 단위의 제곱으로 표현되어 해석이 까다로움
- 제곱근 평균 제곱 오차 (RMSE: Root Mean Squared Error)
장점: MSE의 장점을 유지하면서 원래 단위로 표현
단점: 여전히 이상치에 민감할 수 있음
- 결정 계수 (R²: Coefficient of Determination)
장점: 모델이 데이터의 변동성을 얼마나 잘 설명하는지 나타냄
단점: 독립 변수가 추가될 때마다 증가하는 경향이 있어, 과적합의 위험
3. Nearest Neighbor Classifier
비슷한 입력은 비슷한 출력을 낸다
Nearest Neighbor 알고리즘은 가장 간단하면서도 직관적인 분류 알고리즘 중 하나
알고리즘 동작 원리
학습 -> 모든 훈련 데이터와 그에 해당하는 레이블을 메모리에 저장
예측 -> 새로운 데이터가 주어지면 훈련 데이터와의 거리를 계산
가장 가까운 이웃을 탐색하고 새로운 데이터의 레이블로 예측
거리 측정 방법
- L1 거리 (Manhattan 거리): \(d = Σ|x_i - y_i|\)
특징: 좌표축을 따라 이동하는 거리의 합
- L2 거리 (Euclidean 거리): \(d = √(Σ(x_i - y_i)²)\)
특징: 직선 거리를 측정
- 기타 거리 측정 방법: Minkowski 거리, Mahalanobis 거리 등
k-Nearest Neighbor (k-NN)
Nearest Neighbor 알고리즘의 확장 버전,
가장 가까운 k개의 이웃을 고려하여 다수결로 분류를 수행.
k값의 선택은 모델의 성능에 큰 영향을 줌
- k가 작을 경우: 노이즈에 민감하지만, 복잡한 결정 경계를 만들 수 있음
- k가 클 경우: 더 안정적이지만, 결정 경계가 부드러워져 세부적인 패턴을 놓칠 수 있음
Nearest Neighbor 알고리즘의 장단점
장점:
구현이 간단하고 직관적
훈련 과정이 빠름 (사실상 훈련 과정이 없음)
비선형 결정 경계를 자연스럽게 학습
단점:
예측 시간이 느림 (모든 훈련 데이터와의 거리를 계산해야 함)
메모리 사용량이 많음 (모든 훈련 데이터를 저장해야 함)
차원의 저주: 고차원 데이터에서 성능이 급격히 저하될 수 있음
특성의 스케일에 민감
4. Linear Classifier
입력 데이터를 선형 함수를 사용하여 여러 클래스로 분류하는 알고리즘
입력 특성의 가중치 합을 계산하여 각 클래스에 대한 점수를 산출
\[f(x, W) = Wx + b\]x: 입력 데이터 (예: 이미지의 픽셀 값), W: 가중치 행렬, b: 편향 벡터
- 장점
간단하고 해석하기 쉬움
계산이 효율적 (단일 행렬-벡터 곱으로 예측 가능)
훈련 후에는 가중치 W만 있으면 됨 (메모리 효율적)
- 한계
복잡한 결정 경계를 표현하기 어려움
비선형적 관계를 직접적으로 모델링할 수 없음
Softmax 함수
Linear Classifier를 확률로 변환
\[P(y = k | x) = exp(s_k) / Σ_j exp(s_j)\]s_k는 k번째 클래스에 대한 점수
- 특징
출력값의 범위: 0에서 1 사이
모든 클래스에 대한 확률의 합: 1
지수 함수의 사용으로 클래스 간의 차이를 강조
손실 함수
모델의 예측이 실제 값과 얼마나 다른지를 측정
주요 손실 함수
a) 0/1 손실: 예측이 틀리면 1, 맞으면 0
b) 로그 손실 (Cross Entropy): \(-log(p(y|x))\)
c) 힌지 손실 (Hinge Loss): \(max(0, 1 - yŷ)\)
d) 지수 손실: \(exp(-yŷ)\)
Cross Entropy
분류 문제에서 가장 널리 사용되는 손실 함수
\[L = -Σ_i y_i log(p_i)\]y_i는 실제 레이블, p_i는 예측된 확률
최적화
손실 함수를 최소화하는 모델 파라미터를 찾는 것이 목적
경사 하강법
가장 기본적인 최적화 알고리즘으로, 손실 함수의 기울기를 계산하고 이를 이용해 파라미터를 업데이트
\[θ = θ - α * ∇J(θ)\]α는 학습률, ∇J(θ)는 손실 함수의 그래디언트
Stochastic Gradient Descent (SGD)
전체 데이터셋 대신 무작위로 선택된 일부 데이터(미니배치)를 사용하여 그래디언트를 계산하고 파라미터를 업데이트
장점: 계산 효율성 향상, 큰 데이터셋 적합, 지역 최적해 벗어날 가능성 증가
최적화 과정의 도전 과제
비볼록 최적화 문제: 여러 개의 지역 최적해가 존재할 수 있음
새들 포인트: 그래디언트가 0이지만 최적점이 아닌 지점
느린 수렴 속도: 특히 대규모 데이터셋에서 문제가 될 수 있음